Sign In Sign-Up

Welcome!

Close

Would you like to make this site your homepage? It's fast and easy...

Yes, Please make this my home page!

No Thanks

  Don't show this to me again.

Close

Naturaleza de la resolución de problemas

¿Qué es un problema?

Un problema se define como una situación en la cual un individuo desea hacer algo, pero desconoce el curso de la acción necesaria para lograr lo que quiere (Newell y Simon, 1972), o como una situación en la cual un individuo actúa con el propósito de alcanzar una meta utilizando para ello alguna estrategia en particular (Chi y Glaser, 1983).

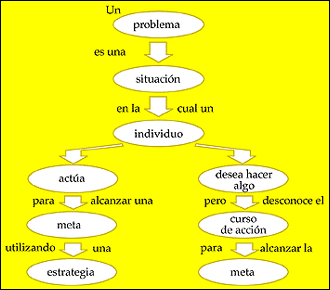
Cuando hacemos referencia a “la meta” o a “lograr lo que se quiere”, nos estamos refiriendo a lo que se desea alcanzar: la solución. La meta o solución está asociada con un estado inicial y la diferencia que existe entre ambos se denomina “problema”. Las actividades llevadas a cabo por los sujetos tienen por objeto operar sobre el estado inicial para transformarlo en meta. De esta manera, se podría decir que los problemas tienen cuatro componentes: 1) las metas, 2) los datos, 3) las restricciones y 4) los métodos (Mayer, 1983).

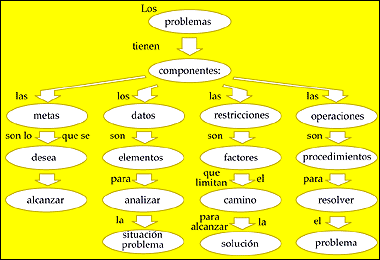
Las metas constituyen lo que se desea lograr en una situación determinada. En un problema puede haber una o varias metas, las cuales pueden estar bien o mal definidas. En general, los problemas de naturaleza matemática son situaciones-problema con metas bien definidas. En el ejemplo: “Alvaro tiene 5 creyones. Javier le dio 8 creyones más. ¿Cuántos creyones tiene Alvaro en total?”, la meta está bien definida, consiste en saber cuántos creyones tiene Alvaro en total, después que Javier le dio 8 creyones. Por el contrario, los problemas de la vida real pueden tener metas no tan claramente definidas.

Los datos consisten en la información numérica o verbal disponible con que cuenta el aprendiz para comenzar a analizar la situación problema. Al igual que las metas, los datos pueden ser pocos o muchos, pueden estar bien o mal definidos o estar explícitos o implícitos en el enunciado del problema. En el ejemplo anterior, los datos están bien definidos y son explícitos: 5 creyones y 8 creyones.

Las restricciones son los factores que limitan la vía para llegar a la solución. De igual manera, pueden estar bien o mal definidos y ser explícitos o implícitos. En el ejemplo anterior, no hay restricciones. Sin embargo, vamos a dar un ejemplo de lo que es una restricción.

Anita tiene una muñeca y quiere vestirla con pantalón y franela. Tiene cuatro pantalones de color rojo, blanco, azul y negro, y tiene tres franelas de color verde, amarillo y rosado. Ella quiere hacer diferentes combinaciones con todos los pantalones y las franelas verde y rosada. ¿Cuántas combinaciones diferentes puede hacer?

En el ejemplo anterior, la restricción consiste en que Anita sólo quiere utilizar dos de las tres franelas, la verde y la rosada, en consecuencia, no todas las franelas van a ser consideradas para las diferentes combinaciones que quiere hacer. Esto es una restricción.

Los métodos u operaciones se refieren a los procedimientos utilizados para resolver el problema. En el caso del ejemplo referido a los creyones, la operación a realizar es una adición, por lo tanto, el solucionador deberá aplicar el algoritmo de la suma.

¿Qué es la resolución de problemas?

Según Dijkstra (1991), la resolución de problemas es un proceso cognoscitivo complejo que involucra conocimiento almacenado en la memoria a corto y a largo plazo.

La resolución de problemas consiste en un conjunto de actividades mentales y conductuales, a la vez que implica también factores de naturaleza cognoscitiva, afectiva y motivacional. Por ejemplo, si en un problema dado debemos transformar mentalmente metros en centímetros, esta actividad sería de tipo cognoscitiva. Si se nos pregunta cuán seguros estamos de que nuestra solución al problema sea correcta, tal actividad sería de tipo afectiva, mientras que resolver el problema, con papel y lápiz, siguiendo un algoritmo hasta alcanzar su solución, podría servir para ilustrar una actividad de tipo conductual. A pesar de que estos tres tipos de factores están involucrados en la actividad de resolución de problemas, la investigación realizada en el área ha centrado su atención, básicamente, en los factores cognoscitivos involucrados en la resolución.

Según Andre (1986), el proceso de resolución de problemas puede describirse a partir de los elementos considerados a continuación:

1. Una situación en la cual se quiere hacer algo, pero se desconocen los pasos precisos para alcanzar lo que se desea.
2. Un conjunto de elementos que representan el conocimiento relacionado con el problema.
3. El solucionador de problemas o sujeto que analiza el problema, sus metas y datos y se forma una representación del problema en su sistema de memoria.
4. El solucionador de problemas que opera sobre la representación para reducir la discrepancia entre los datos y las metas. La solución de un problema está constituida por la secuencia de operaciones que pueden transformar los datos en metas.
5. Al operar sobre los datos y las metas, el solucionador de problemas utiliza o puede utilizar los siguientes tipos de información:
   • Información almacenada en su memoria de largo plazo en forma de esquemas o producciones.
   • Procedimientos heurísticos.
   • Algoritmos.
   • Relaciones con otras representaciones.
6. El proceso de operar sobre una representación inicial con el fin de encontrar una solución al problema, se denomina búsqueda. Como parte del proceso de búsqueda de la solución, la representación puede transformarse en otras representaciones.
7. La búsqueda continúa hasta que se encuentra una solución o el solucionador de problemas se da por vencido.

Etapas de la resolución de problemas

Varios investigadores han analizado la actividad de resolución de problemas y señalan que tal actividad es un proceso que involucra una serie de etapas. Desde principios de siglo se viene investigando sobre las fases en la resolución de problemas. Es así como Wallas (1926) señala que éstas incluyen las siguientes:

1. La preparación, es la fase en la cual el solucionador analiza el problema, intenta definirlo en forma clara y recoge hechos e información relevante al problema.
2. La incubación, es la fase en la cual el solucionador analiza el problema de manera inconsciente.
3. La inspiración, es la fase en la cual la solución al problema surge de manera inesperada.
4. La verificación, es la fase que involucra la revisión de la solución.

Otros autores (Andre, 1986; Hayes, 1981) señalan que las etapas en la resolución de problemas sirven para enfatizar el pensamiento consciente y para aproximarse analíticamente a la solución, así como también para ofrecer una descripción de las actividades mentales de la persona que resuelve el problema. En tal sentido, Andre (1986) propone que las etapas en la resolución de problemas son las especificadas en el cuadro 1:

Es de hacer notar que las etapas se aplican usualmente a problemas aritméticos y algebraicos, pero también pueden aplicarse a muchos otros tipos de problemas no necesariamente relacionados con disciplinas académicas.

Por su parte, Polya (1965) señala que un problema puede resolverse correctamente si se siguen los siguientes pasos:

• Comprender el problema.
• Concebir un plan para llegar a la solución.
• Ejecutar el plan.
• Verificar el procedimiento.
• Comprobar los resultados.

Schoenfeld (1985), a partir de los planteamientos de Polya (1965), se ha dedicado a proponer actividades de resolución de problemas que se pueden llevar a cabo en el aula, con el fin de propiciar situaciones semejantes a las condiciones que los matemáticos experimentan en el proceso de desarrollo de resolución de problemas. Su modelo de resolución abarca los siguientes pasos: Análisis, Exploración y Comprobación de la solución y puede aplicarse a problemas matemáticos y algebraicos. Aunque estos pasos no necesariamente tienen que ser aplicados en su totalidad, en el Anexo 1 se incluye un ejemplo de resolución de un problema matemático siguiendo este modelo.

Análisis

1. Trazar un diagrama, si es posible.
2. Examinar casos particulares
3. Probar a simplificar el problema

Exploración

1. Examinar problemas esencialmente equivalentes: sustituir las condiciones por otras equivalentes, recombinar los elementos del problema de modo diferente, replantear el problema.
2. Examinar problemas ligeramente modificados: establecer submetas, descomponer el problema en casos y analizar caso por caso.
3. Examinar problemas ampliamente modificados: construir problemas análogos con menos variables, mantener fijas todas las variables menos una para determinar qué efectos tiene esa variable, tratar de sacar partido de problemas afines que tengan parecido en su forma, en sus datos o en sus conclusiones.

Comprobación de la solución obtenida

1. Verificar la solución obtenida siguiendo criterios específicos: utilización de todos los datos pertinentes, uso de estimaciones o predicciones.
2. Verificar la solución obtenida siguiendo criterios generales: examinar la posibilidad de obtener la solución por otro método, reducir la solución a resultados conocidos.

En síntesis, como puede observarse, desde principios de este siglo, diferentes autores han propuesto pasos, fases o etapas a cumplir para poder resolver problemas con éxito. Este aspecto es importante ya que permite, de antemano, planificar los pasos a seguir en la resolución de un problema, ejecutar esos pasos y, posteriormente, supervisar el proceso de resolución y comprobar la solución o resultado.

PÁG. PRINCIPAL